Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst-case complexity are O(n²), respectively.

Partition in Quick Sort

Following animated representation explains how to find the pivot value in an array.

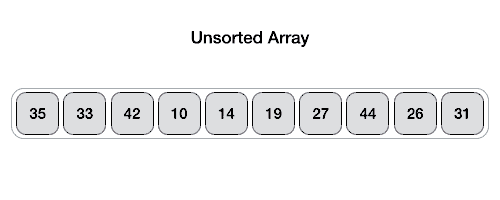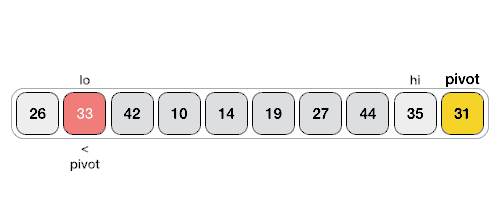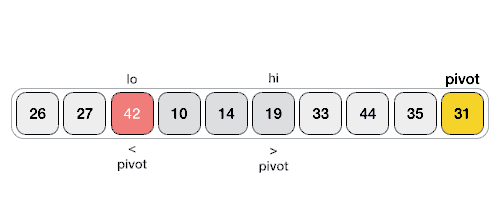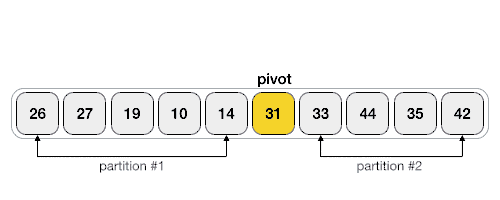
The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element.

Quick Sort Pivot Algorithm

Based on our understanding of partitioning in quick sort, we will now try to write an algorithm for it, which is as follows.

Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot

Quick Sort Pivot Pseudocode

The pseudocode for the above algorithm can be derived as −

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do
         //do-nothing            
      end while
		
      while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
		
   end while 
	
   swap leftPointer,right
   return leftPointer
	
end function

Quick Sort Algorithm

Using pivot algorithm recursively, we end up with smaller possible partitions. Each partition is then processed for quick sort. We define recursive algorithm for quicksort as follows −

Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively

Quick Sort Pseudocode

To get more into it, let see the pseudocode for quick sort algorithm −

procedure quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
   
end procedure

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Implementation in C

#include <stdio.h>
#include <stdbool.h>

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      printf("%d ",intArray[i]);
   }
	
   printf("]\n");
}

void swap(int num1, int num2) {
   int temp = intArray[num1];
   intArray[num1] = intArray[num2];
   intArray[num2] = temp;
}

int partition(int left, int right, int pivot) {
   int leftPointer = left -1;
   int rightPointer = right;

   while(true) {
      while(intArray[++leftPointer] < pivot) {
         //do nothing
      }
		
      while(rightPointer > 0 && intArray[--rightPointer] > pivot) {
         //do nothing
      }

      if(leftPointer >= rightPointer) {
         break;
      } else {
         printf(" item swapped :%d,%d\n", intArray[leftPointer],intArray[rightPointer]);
         swap(leftPointer,rightPointer);
      }
   }
	
   printf(" pivot swapped :%d,%d\n", intArray[leftPointer],intArray[right]);
   swap(leftPointer,right);
   printf("Updated Array: "); 
   display();
   return leftPointer;
}

void quickSort(int left, int right) {
   if(right-left <= 0) {
      return;   
   } else {
      int pivot = intArray[right];
      int partitionPoint = partition(left, right, pivot);
      quickSort(left,partitionPoint-1);
      quickSort(partitionPoint+1,right);
   }        
}

int main() {
   printf("Input Array: ");
   display();
   printline(50);
   quickSort(0,MAX-1);
   printf("Output Array: ");
   display();
   printline(50);
}

If we compile and run the above program, it will produce the following result:

Output

Input Array: [4 6 3 2 1 9 7 ]
==================================================
 pivot swapped :9,7
Updated Array: [4 6 3 2 1 7 9 ]
 pivot swapped :4,1
Updated Array: [1 6 3 2 4 7 9 ]
 item swapped :6,2
 pivot swapped :6,4
Updated Array: [1 2 3 4 6 7 9 ]
 pivot swapped :3,3
Updated Array: [1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================